Power over power, speed over speed

• A good site with some useful images
• A short-ish YouTube video,

Binary operations and registers

This is a more detailed explanation of what was covered in the meeting

Binary numbers

Binary numbers are base 2 - the only valid digits are 0 (”setting” a bit) and 1(”clearing” a bit). Computers operate in binary, using a high and low voltage to represent each value; this makes it less likely that a fluctuation will be read as the wrong value.

Also used often in computing are hexadecimal numbers (base 16), ranging from 0 to 9, and then continuing with the first 6 letters (A through F) before restarting. Computers still convert these values to binary, but “hex” is a more compact way to represent it. 1 hex digit = 4 binary digits (C == 1100)

Some common written formats for the decimal number 29, and how to calculate them:

• Decimal: $\texttt{29}$, $29_{10}$
  • $2 \times 10^1 + 9 \times 10^0 = 20 + 9 = 29$
• Binary: $\texttt{11101}$, $\texttt{11101}_\texttt{2}$, $\texttt{0b11101}$
  • $1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 16 + 8 + 4 + 0 + 1 = 29$
• Hexadecimal: $\texttt{1D}$, $\texttt{1D}_\texttt{16}$, $\texttt{0x1D}$
  • $1 \times 16^1 + (9 + 4) \times 16^0 = 16 + 13 = 29$

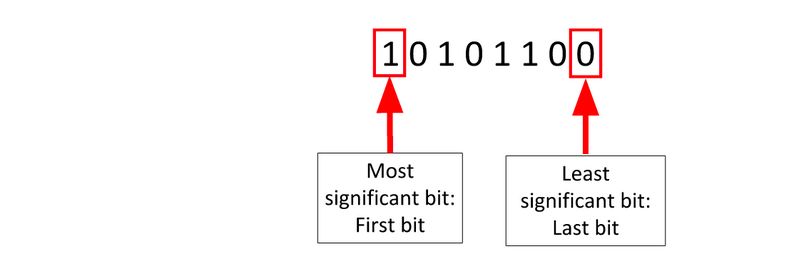
Negative numbers can also be represented in binary, but there are a few different way to do it. The most common is two’s complement, which uses the most significant bit (see right) to indicate positive (0) or negative (1). Here’s two ways to calculate the two’s complement of 30, which equals $\text{-30}$:

Also abbreviated to MSB and LSB, respectively.

0b011110 --> 0b100001 // Flip all bits

  0b100001
+ 0b000001 // Notice the inclusion of the extra MSB to indicate a positive number
----------
  0b100010

// Adding both numbers should equal 0
  0b011110 // positive
+ 0b100010 // negative
----------
  0b000000

// The sign bit can be extended, so the carry over continues infinitely, and is ignored
0b011101 == 0b0000000000011101
0b100010 == 0b1111111111100010

0b011110 // The least significant one is in the 2nd spot from the right
// Flip all bits to the left of it

0b0111 10 -> 0b1000 10 -> 0b100010

// Check
  0b011110
+ 0b100010
----------
  0b000000

And lastly, a useful tip: 0x5 == 0b0101 and 0xA == 0b1010

Bitwise operations

You can also perform bitwise (logical) operations. These are similar to operations performed in if() or for() statements, but they operate on a bit-by-bit basis. You can use binary numbers as bitmasks to perform operations on many bits at the same time